Push Block
Approach
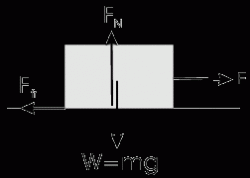
The force that is applied is just sufficient to over the static friction. The acceleration is zero. So the applied force plus the force of friction is zero by Newton's Second Law of motion.
Solution
Since the force, 17.7 N, is just enough to start the block moving, the acceleration of the block is zero. Thus...
F-Ffr = 0
where F*fr = μs*FN = μs*m*g since from the diagram, FN = mg. Thus
us= F/mg = 17.69/(3.5*9.8)=0.515
F-Ffr = 0
where F*fr = μs*FN = μs*m*g since from the diagram, FN = mg. Thus
us= F/mg = 17.69/(3.5*9.8)=0.515
Part B
Approach
Once the block starts moving, the kinetic friction takes over. (Kinetic friction is less than the static friction - that is why it is hard to get an object to move but once it starts moving, it keeps moving with the same force.) This results a net force which according to Newton's Second Law gives rise to the acceleration.
Solution
Newton's Second Law of motion - sum of the net force equals to the mass times acceleration...
F-Ffr = m*a
where Ffr = μkFN = μkmg. Thus...
us = (F-m*a)/(m*g) = (17.68 - (3.5*0.83))/(3.5*9.81) = 0.43
F-Ffr = m*a
where Ffr = μkFN = μkmg. Thus...
us = (F-m*a)/(m*g) = (17.68 - (3.5*0.83))/(3.5*9.81) = 0.43