Medieval Castle
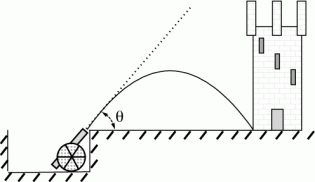
Assume you are a Medieval knight attacking a castle with a cannon. The ball leaves the cannon with a speed of 48.3 m/s. The barrel's angle with respect to the ground is 38.1°, and you make a perfect hit on the tyrant's chamber which is at the same level as the cannon's muzzle.
What is the time of flight of the cannon ball?
6.08 s
What is the time of flight of the cannon ball?
6.08 s
Disussion
Anonymous 2 (Wed Jan 20 11:06:24 pm 2010 (EST))
how do you find the height the cannon ball reaches?
NEW
Anonymous 3 (Thu Jan 21 05:23:06 pm 2010 (EST))
can someone point me in the right direction to start this?
NEW
know velocity and angle, so use the equation from 4.23 in
the book to find time to the top of the arc, then have to
double it.
NEW
the equation you would use to find ymax would be:
ymax= Vo*sin/g
Initial velocity times the sin of the angle made by the
ground and the projectile divided by gravity (9.8m/s^2)
sense the cannon lands at the same level it is projected
you can multiply the previous equation by two to get total
hang time.
NEW
Anonymous 2 (Thu Jan 21 09:13:11 pm 2010 (EST))
that is exactly what i did but it isn't accepting my
answer..any suggestions?
NEW
You're trying to find the max height (ymax). Since you know
your angle (theta), you can obtain ymax by using sin(theta)
= ymax/initial velocity. However, you have to factor in the
force of gravity, so your final equation becomes:
Ymax = Initial velocity x [sin(theta)/9.8]
NEW
Oh, and then multiply the answer to what I just posted by
two, since you have to account for the descent of the
cannonball as well.
NEW
If someone could give another explanation to solve this that
would be great! I've tried the other equations and still am
not getting the correct answer
NEW
make sure your calculator is set to deg.
how do you find the height the cannon ball reaches?
NEW
Anonymous 3 (Thu Jan 21 05:23:06 pm 2010 (EST))
can someone point me in the right direction to start this?
NEW
know velocity and angle, so use the equation from 4.23 in
the book to find time to the top of the arc, then have to
double it.
NEW
the equation you would use to find ymax would be:
ymax= Vo*sin/g
Initial velocity times the sin of the angle made by the
ground and the projectile divided by gravity (9.8m/s^2)
sense the cannon lands at the same level it is projected
you can multiply the previous equation by two to get total
hang time.
NEW
Anonymous 2 (Thu Jan 21 09:13:11 pm 2010 (EST))
that is exactly what i did but it isn't accepting my
answer..any suggestions?
NEW
You're trying to find the max height (ymax). Since you know
your angle (theta), you can obtain ymax by using sin(theta)
= ymax/initial velocity. However, you have to factor in the
force of gravity, so your final equation becomes:
Ymax = Initial velocity x [sin(theta)/9.8]
NEW
Oh, and then multiply the answer to what I just posted by
two, since you have to account for the descent of the
cannonball as well.
NEW
If someone could give another explanation to solve this that
would be great! I've tried the other equations and still am
not getting the correct answer
NEW
make sure your calculator is set to deg.