Chain
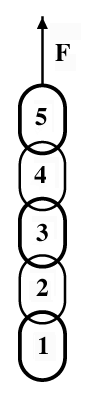
A chain consisting of five links, each of mass 0.200 kg, is lifted vertically with a constant acceleration of a = 2.8 m/s2.
Find the magnitude of the force that link 3 exerts on link 2.
5.04 N
What is the magnitude of the force F that must be exerted on the top link to achieve this acceleration?
1.26×101 N
Find the magnitude of the force that link 3 exerts on link 2.
5.04 N
What is the magnitude of the force F that must be exerted on the top link to achieve this acceleration?
1.26×101 N
Discussion
Anonymous 1 (Thu Jan 21 05:20:26 pm 2010 (EST))
could someone explain this problem? I know it is easy.. i think i am over
thinking it
NEW
use:
F-mg=ma
and solve for the force F
F=force N
m=mass kg
g=9.80 m/s^2
a=acceleration m/s^2
in part one your mass is the combined mass of however many links the force is exerted on and doesn't count the links above it.
example: how much force does link 3 exert on link 2. link 3 has to exert a foce on the mass of link 2 plus the mass of link 1 because if you pull up link 2 link one comes with it. so your mass is the mass of link 1 and two combined
in part two use the same equation as b4 ecxept your mass is the entire weight of all the links combined, at least my question asked for the force exerted on the top link. So the mass includes that of the top link and all links connected below it. Than solve for F as in part one.
The only thing that changes is the mass value.
NEW
Re: Re: Anonymous 3 (Fri Jan 22 02:52:08 pm 2010 (EST))
I got the second part right by using the mass of all 5
links for ma and mg. But I cant get the first part, I
understand that we use the mass of link 1 and 2 combined
when we calculate mg but what about for ma?
NEW
I am so frustrated I have tried everything...
I have
F(2,3)-mg=2mxA:
F-9.8=2(.125)x2.3 or F-(.125)(9.8)=2(.125)(2.3) or F-
2(.125)(9.8)=2(.125)(2.3)....
none of these have given me the right answer and that's even the equation he
gave us in recitation and I still can't understand why none of these have
worked. Can anyone direct me to where I'm making a mistake?
NEW
The force that link 3 exerts on link 2 must lift both links
1 and 2. So the mass of these links is
.
m = 0.175 + 0.175 = 0.350 kg
.
And we know: upward force - mg = ma
.
upward force = ma + mg = 0.350 * 2.70 + 0.350 *
9.80 = 4.375 N is the force link 3 exerts on link 2
.
The top force must lift all five links, a total mass of m
= 5 * 0.175 = 0.875 kg
.
so F = ma + mg = 0.875 * 2.70 + 0.875 * 9.80 =
10.9375 N
could someone explain this problem? I know it is easy.. i think i am over
thinking it
NEW
use:
F-mg=ma
and solve for the force F
F=force N
m=mass kg
g=9.80 m/s^2
a=acceleration m/s^2
in part one your mass is the combined mass of however many links the force is exerted on and doesn't count the links above it.
example: how much force does link 3 exert on link 2. link 3 has to exert a foce on the mass of link 2 plus the mass of link 1 because if you pull up link 2 link one comes with it. so your mass is the mass of link 1 and two combined
in part two use the same equation as b4 ecxept your mass is the entire weight of all the links combined, at least my question asked for the force exerted on the top link. So the mass includes that of the top link and all links connected below it. Than solve for F as in part one.
The only thing that changes is the mass value.
NEW
Re: Re: Anonymous 3 (Fri Jan 22 02:52:08 pm 2010 (EST))
I got the second part right by using the mass of all 5
links for ma and mg. But I cant get the first part, I
understand that we use the mass of link 1 and 2 combined
when we calculate mg but what about for ma?
NEW
I am so frustrated I have tried everything...
I have
F(2,3)-mg=2mxA:
F-9.8=2(.125)x2.3 or F-(.125)(9.8)=2(.125)(2.3) or F-
2(.125)(9.8)=2(.125)(2.3)....
none of these have given me the right answer and that's even the equation he
gave us in recitation and I still can't understand why none of these have
worked. Can anyone direct me to where I'm making a mistake?
NEW
The force that link 3 exerts on link 2 must lift both links
1 and 2. So the mass of these links is
.
m = 0.175 + 0.175 = 0.350 kg
.
And we know: upward force - mg = ma
.
upward force = ma + mg = 0.350 * 2.70 + 0.350 *
9.80 = 4.375 N is the force link 3 exerts on link 2
.
The top force must lift all five links, a total mass of m
= 5 * 0.175 = 0.875 kg
.
so F = ma + mg = 0.875 * 2.70 + 0.875 * 9.80 =
10.9375 N